教学目标

1、理解除法的概念及余数和除数的定义。

2、掌握余数和除数之间的关系，并能运用在实际问题中。

3、培养学生的逻辑思维能力和数学运算能力。

1、除法的概念及定义

2、余数和除数的定义

3、余数和除数之间的关系

4、余数定理的应用

教学重难点

重点：余数和除数之间的关系。

难点：余数定理的应用。

教学准备

1、黑板或多媒体设备，用于展示教学内容。

2、练习题目，用于课堂练习和巩固知识。

教学过程

（一）导入新课

通过回顾除法的概念，引出余数和除数的概念，为学习余数和除数的关系做好铺垫。

（二）新课讲解

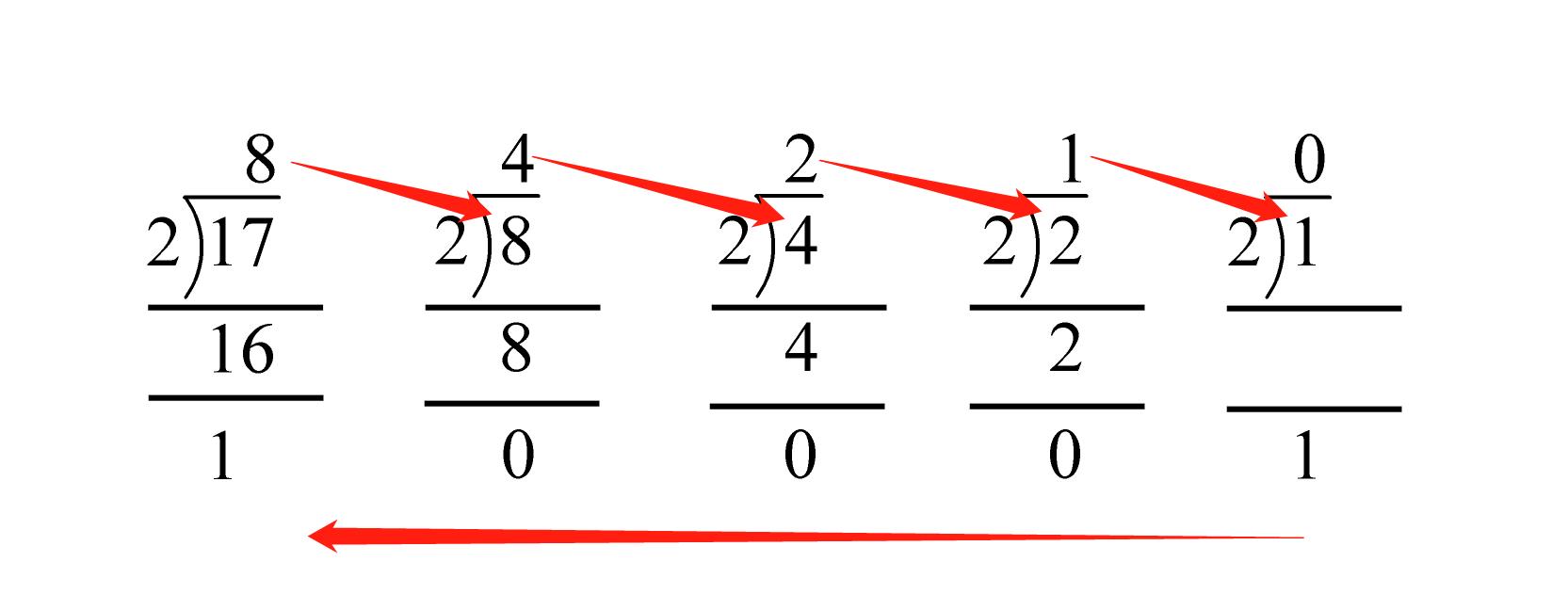
1、除法的概念及定义：除法是一种数学运算，表示将一个数（被除数）分成若干份（商），每份相等，并可能剩余一部分（余数），17÷5=3……2，17是被除数，5是除数，3是商，2是余数。

2、余数和除数的定义：在除法运算中，余数是指被除数除以除数后剩余的部分，除数是用来分割被除数的数，在上面的例子中，余数是2，除数是5。

3、余数和除数之间的关系：余数一定小于除数，这是因为如果余数等于或大于除数，那么就可以继续除以除数，商会增加，如果余数为除数或大于除数时，我们可以继续除以除数得到新的商和余数，余数和除数之间存在一定的关系，我们可以通过这个关系来判断除法运算的结果是否准确，如果已知除数和余数，我们可以判断商是否准确；或者已知除数和商，我们可以求出余数等，这些关系在实际问题中有广泛的应用，在密码学中，我们常常利用余数的性质来加密和解密信息；在计算机科学中，利用余数定理实现循环数组等数据结构等，因此掌握余数和除数之间的关系是非常重要的，我们可以通过具体的例子来进一步理解这个关系，假设我们有一个数n除以一个数m得到余数r那么我们可以表示为n=mq+r其中q是商r是余数且r小于m这就是余数定理的应用之一可以帮助我们解决很多实际问题，通过讲解和举例让学生充分理解余数和除数之间的关系并能够运用在实际问题中，同时可以通过练习题来巩固知识提高应用能力。（三）课堂练习布置相应的练习题让学生完成如：已知一个数除以一个数得到的商和余数求被除数；已知被除数和商求余数等题目让学生加深对余数和除数关系的理解。（四）总结回顾今天学习的内容总结余数和除数的概念及关系强调余数一定小于除数并举例说明余数和除数之间的关系在实际问题中的应用。（五）布置作业布置相关练习题让学生回家完成巩固今天所学的知识。（六）教学反思通过本次教学总结本次教学的优点和不足分析学生的学习情况调整教学策略以提高教学质量，六、教学评价采用课堂表现、作业完成情况、小测验等方式对学生的学习情况进行评价了解学生对余数和除数关系的掌握情况以便及时调整教学策略提高教学效果，同时鼓励学生积极参与课堂讨论和练习培养逻辑思维能力和数学运算能力，七、教学意义通过本次教学使学生理解除法的概念及余数和除数的定义掌握余数和除数之间的关系并能运用在实际问题中培养学生的逻辑思维能力和数学运算能力为今后的学习和生活打下坚实的基础，八、教学建议在教学过程中应注重启发式教学引导学生自主思考、探究问题；同时结合实际例子讲解知识点使学生更好地理解和应用知识；鼓励学生多练习多做题提高运算能力和解题能力；关注学生的个体差异因材施教以满足不同学生的学习需求，九、教学拓展与延伸1. 可以引导学生探究余数和除数关系的更深层次性质如费马小定理等拓展学生的视野激发学习兴趣，2. 可以结合计算机编程相关知识点讲解余数定理的应用如循环数组、哈希表等帮助学生更好地理解数学在实际应用中的作用，十、教学案例举例案例一：已知一个数27除以一个数m得到的商是4求m的值？分析：根据除法定义我们知道被除数等于除数乘以商加余数即被除数=除数×商+余数由此我们可以列出方程求解得到m的值案例二：已知一个数n除以一个数m得到的余数是r求n的值分析：根据余数定理我们知道n等于除数乘以商加余数即n=mq+r通过已知条件我们可以求出n的值案例三：已知一个数n和一个数m求两数相除的余数分析：我们可以通过计算两数的差来判断它们的最大公约数进而求出它们的余数这个知识点在计算机科学中有广泛的应用如判断两个数是否互质等，通过以上案例的讲解和练习使学生更好地理解和掌握余数和除数之间的关系并能够运用在实际问题中。